Hier kann ein Programm gewählt werden, mit dem ein System von n linearen

Gleichungen online gelöst werden kann.

Mit reellen Zahlen

Mit komplexen Zahlen

Anwendungsbeispiele im Mathematikunterricht

Für die Summe S aller ganzen Zahlen von 1 bis n gilt: S = n· (1 + n) / 2 = ½ · n + ½ · n² .

Diese Gleichung ist leicht ableitbar.

Die Herleitung entsprechender Gleichungen für die Summen S = 1² + 2² + 3² + 4²......+ n² und S = 1³ + 2³+ 3³ + 4³......+ n³ ist mit dem hier vorliegenden Programm nicht schwieriger. Sie gelingt wie folgt:

Angesichts S = ½ · n + ½ · n² für 1+2+3...+n liegt die Vermutung nahe, dass für S = 1² + 2² + n² gilt: S = a · n + b · n² + c · n³. Die unbekannten Faktoren a , b und c müssen ermittelt werden. Dies geschieht mit den 3 Gleichungen:

a · 1 + b · 1² + c · 1³ = 1

a · 2 + b · 2² + c · 2³ = 5

a · 3 + b · 3² + c · 3³ = 14

a , b und c sind als die Unbekannten x(1), x(2) und x(3) zu sehen. Als Lösung erhält man mit dem genannten Programm: x(1) = 0,1666666, x(2) =0,5 und x(3) = 0,33333. Die 3 Werte stehen für die Brüche: 5/30 = 1/6, 1/2 und 1/3.

↓

S = 1/6 · n +1/2 · n² + 1/3· n³ = 1/6 · (n + 3· n² + 2· n³ ).

Zur Bestimmung einer Summenformel für 1³ + 2³+ 3³ + 4³......+ n³ müssen 4 Gleichungen aufgestellt werden.

1³ + 2³+ 3³ + 4³......+ n³ = ¼ ·(n² + 2 · n³ + n⁴ ) ist in diesem Fall das Ergebnis der Rechnung .

Mit dem „Schluss von n auf n+1“ können diese Gleichungen mühelos bewiesen werden.

Mit dem Programm Polynome können die gewonnenen Gleichungen noch schneller gefunden werden. Dieses Programm erstellt anhand n gegebener x,y_Wertepaare ein zu einem Polynom n-1.Grades passendes System von Gleichungen selbst und löst dieses.

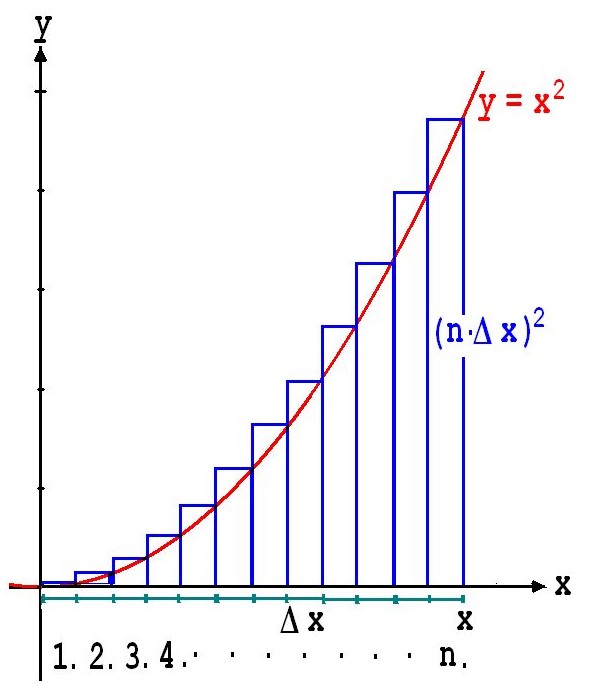
S = 1/6 · (n + 3· n² + 2· n³ ) für 1² + 2² + 3²... erweist sich bei der Einführung des Integralbegriffs als sehr nützlich. Da wird zunächst die Frage gestellt, wie der Flächeninhalt einer Fläche A bestimmt werden kann, die wie in der folgenden Abbildung von einem Funktionsgraphen z.B. dem zu y = f(x) = x², dann der x-Achse und einer parallel zur y-Achse verlaufenden Geraden eingegrenzt wird.

Der Fläche A werden, wie in der Abbildung sichtbar, Rechtecke angepasst, deren gesamter Flächeninhalt zu einer etwas groben Beschreibung von A geeignet ist. Die hier sichtbaren Rechtecke von 1 bis n haben zusammen den Flächeninhalt:

S = Δx· (1·Δx)² + Δx· (2·Δx )² + Δx· (3·Δx )².........+ Δx· (n·Δx )²

S = Δx³· (1 + 2² + 3².........+ n²) = Δx³·1/6 · (n + 3· n² + 2· n³ ), Δx = x/n

↓

S = x³ ·1/6 · (1/n² + 3/n + 2)

Wird die Aufteilung des Abschnitts von 0 bis x mit zunehmendem n schrittweise verfeinert , dann passt sich die aus den Rechtecken gebildete Fläche immer besser der Fläche A an. S strebt gegen den Wert 1/3 · x³. Dieser Grenzwert ∑f(x)·Δx_{( Δx → 0)} , der in dem hier behandelten Fall für einen Flächeninhalt steht, wird Integral ₀∫^xf(x)dx genannt.

Im Fall f(x) = x³ erhält man für ₀∫^xf(x)dx mit der für 1³ + 2³+ 3³ + 4³......+ n³ geltenden Summenformel S =¼ ·(n² + 2 · n³ + n⁴ ) den Wert ₀∫^xf(x)dx = 1/4 · x⁴.