Programm zur Bestimmung der Zentripetalbeschleunigung



Wie in Abb. 1 angedeutet, rotiert eine Kugel B in einer auf der Experimentierwippe stehenden Schale mit konstanter Winkelgeschwindigkeit ω auf einer Bahn mit dem Radius r. ω = 2·π / T (T= Zeit einer Drehung). Das Diagramm zu y=r·sin(ω·t) in der Abb. 2 beschreibt die Bewegung des Punktes P, der senkrechten Projektion des Körpers B auf einen durch den Kreismittelpunkt gehenden Pfeil (y-Achse des zugeordneten Koordinatensystems). Die Beschleunigung von P bei sehr kleiner Abweichung s vom Punkt A zeigt an, wie B zum Kreismittelpunkt hin beschleunigt wird. Diese Beschleunigung a wird Zentripetalbeschleunigung genannt. Die beschleunigende Kraft m·a heißt Zentripetalkraft (m: Masse von B). Zur Bestimmung der Beschleunigung wird dem Bewegungsdiagramm von P ein Bewegungsdiagramm einer bei A beginnenden gleichförmig-beschleunigten Bewegung in Pfeilrichtung (s = b·t'2 ) angepasst (t': Zeit für den Weg s). Der Faktor b = (a/2) wird so gewählt, dass beide Diagramme sich bei kleinem s kaum unterscheiden (siehe Abb.2), dass demnach die zu s=b·t'2 passende Bewegung bei kleinem s mit der Bewegung von P übereinstimmt. Mit a = 2·b erhält man so die Beschleunigung von P bei A. Dies ist die Zentripetalbeschleunigung.

Mit diesem Programm (siehe unten) können Messungen mit frei wählbaren Radien r und Winkelgeschwindigkeiten ω vorgenommen werden. So kann gezeigt werden, dass für die Zentripetalbeschleunigung gilt: a = ω2 · r = v2 /r.

Abb.1



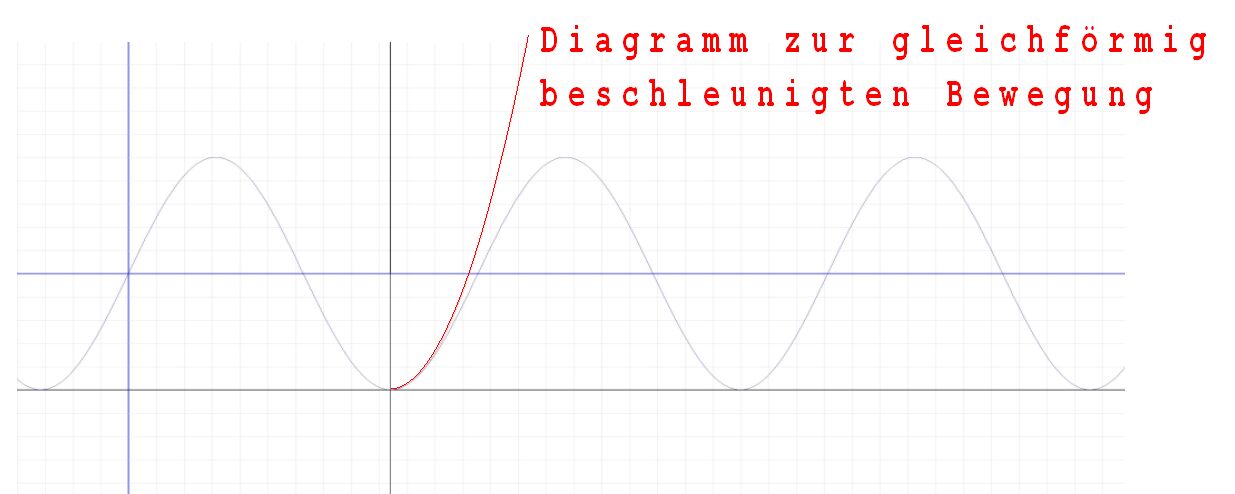
Abb.2





Beschreibung des Diagrammfeldes

Einheiten in horizontaler Richtung=     Einheiten in vertikaler Richtung=

Länge einer waagrechten Einheit in Pixel=    Länge einer senkrechten Einheit in Pixel=

Abstände des zum Koordinatensystem gehörenden Nullpunkts vom linken und unteren Rand des Bildfeldes

Abstand vom linken Rand=     Abstand vom unteren Rand=



Zahlen mit Dezimalpunkt und nicht mit Dezimalkomma eingeben !


Für den y-Wert von P gilt: y = r·sin(ω·t).



r =  m,     ω =  1/s


s = b·t'2 = (a/2)·t'2


  b=   m/s2





Der Funktionsterm der Parabel, welche die Bewegung der Projektion P bei kleinem s beschreibt, soll nun anhand der Abb.3 hergeleitet werden. Das Dreieck ABC ist nach dem Satz des Thales ein rechtwinkliges Dreieck. In der Zeit t' legt P während der Kreisbewegung von A nach B den Weg s zurück. Der Kreisbogen AB weicht bei kleinem t' nur sehr wenig von der Kathete AB ab. Es gilt somit nach dem Kathetensatz:

s· (2 · r) = ( v·t')2 → s = [(v2/r) /2]·t'2 , s = (a /2) · t'2 → a = v2/r


v = 2·π·r / T, ω= 2·π / T  → v = ω ·r → a = ω2 ·r



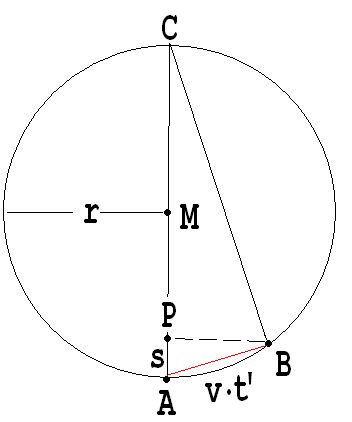
Abb. 3