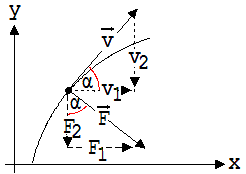
Bewegung unter einer konstanten Normalkraft

Wenn eine Kraft auf einen Körper K wirkt, erwartet man an K eine Veränderung des Geschwindigkeitsbetrags. Dies ist nicht immer der Fall, z.B. dann nicht, wenn es sich um eine Normalkraft handelt, wenn die Bewegungsrichtung mit der Richtung der Kraft einen rechten Winkel bildet. Man denke an einen Körper der Masse m, der an einem Faden auf einer Kreisbahn geführt wird.

Wir untersuchen nun eine solche Bewegung in der x-y-Ebene unter einer dem Betrage nach konstanten Normalkraft F = {F₁ ; F₂ ; 0}. In der Schule ist die mathematische Behandlung dieser Bewegung nur mit Hilfe eines Rechners möglich. Hierbei wird in folgender Weise vorgegangen:

Die Bewegungszeit wird in sehr kleine Zeitabschnitte Δt zerlegt. Ein Δt ist so klein, dass innerhalb dieses Δt die Kraft nach Richtung und Betrag als konstant angesehen werden kann. Mit den für konstante Kräfte geltenden Bewegungsgleichungen wird die Änderung des Orts und der Geschwindigkeit während des ersten Zeitabschnitts Δt berechnet.

a₁ = F₁ /m, a₂ = F₂ /m

F₁, F₂ : Kraftkomponenten während des Zeitabschnitts Δt

a₁, a₂: Beschleunigungen in x- und y-Richtung

v₁ = a₁· Δt + u₁ , v₂ = a₂· Δt + u₂

u₁, u₂ : Geschwindigkeiten vor Δt, v₁, v₂ : Geschwindigkeiten nach Δt

x = 0,5 · a₁ · Δt² + u₁ · Δt + x₀ , y = 0,5 · a₂ · Δt² + u₂ · Δt + y₀

x₀, y₀: Koordinaten vor Δt, x, y: Ortskoordinaten nach Δt

Nach dieser Rechnung ist der Ort und die Geschwindigkeit zu Beginn des zweiten Abschnitts Δt bekannt. Mit deren Werten wird daraufhin der Ort und die Geschwindigkeit zu Beginn des dritten Abschnitts ( nach dem Ende des 2. Abschnitts) berechnet usw..

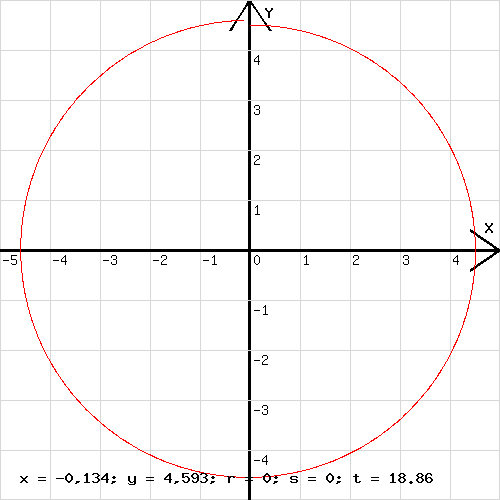
Manchmal ist auch eine Angabe über die Bewegungszeit erwünscht. Hat diese vor Δt den Wert t_vor , dann ist sie nach Δt gleich t_nach = t_vor +Δt.

Zur Untersuchung der Bewegung wird die folgende Zeile in das Fenster des hier vorliegenden Programms geschrieben:

k=0,5; h=0,01; m=1; i=wrz(c^2+d^2); f=k*d/i; g=-k*c/i; a=f/m; b=g/m; x=0,5*a*h^2+c*h+x; y=0,5*b*h^2+d*h+y ; c=c+a*h; d=d+b*h; l=l+1; t=t+h

k = F , f = F_x, g = F_y, c = v₁, d =v₂, h = Δt

Mit dieser Zeile wurde die Bahn in der Abb.2 erhalten. Im Variablenfeld wurde für v₁ = c der Wert 1,5 (1,5 m/s) und für F = k der Wert 0,5 (0,5 N) eingetragen. Mit der Eingabe n =1886 wurde festgelegt, dass die eingetragene Zeile 1886 Mal bearbeitet wird, dass somit 1886 Punkte gezeichnet werden. Die Bearbeitung wird beendet wenn l (L) in der Programmzeile größer als n ist. Die in der Abb. 2 sichtbare Bahn weicht etwas von einer Kreisbahn ab. Dies ist auf Rechenungenauigkeiten zurückzuführen. Eine höhere Rechengenauigkeit wird erreicht, wenn zur Berechnung statt der Beschleunigung zu Beginn eines kleinen Zeitabschnitts Δt die Beschleunigung in der Mitte von Δt genommen wird. Für die Änderung Δa der Beschleunigung in Δt/2 kann geschrieben werden:

Δa ≈ (a_{nach Δt} – a_{vor Δt} ) / 2 → a_Mitte ≈ a_{vor Δt} + (a_{nach Δt} – a_{vor Δt} ) / 2

Da a_{nach Δt} zunächst unbekannt ist, ist eine solche Korrektur für das erste Δt nicht möglich. Für die folgenden Zeitabschnitte werden die Δa - Werte genommen, die für den jeweils vorangehenden Zeitabschnitt ermittelt wurden. Dies geschieht mit der folgenden Anweisungen an den Rechner:

k=0,5; h=0,01; m=1; i=wrz(c^2+d^2); f=k*d/i; g=-k*c/i; a=f/m; b=g/m; a=0,5*j*(a-o)+a;b=0,5*j*(b-p)+b; x=0,5*a*h^2+c*h+x; y=0,5*b*h^2+d*h+y ; c=c+a*h; d=d+b*h; o=a;p=b; l=l+1; j=1; t=t+h

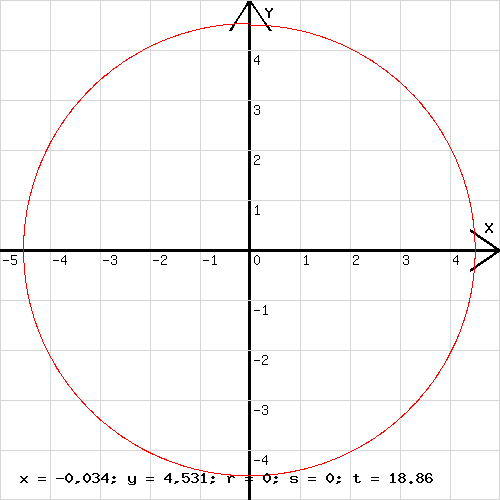
Mit a = 0,5 * j * (a - o) + a; b = 0,5 * j * (b - p) + b; wird die Korrektur vorgenommen. o und p sind Beschleunigungen zu Beginn des vorangehenden Zeitabschnitts Δt. Da solche Werte beim ersten Δt nicht vorliegen, müssen 0,5 * (a – o) und 0,5 * (b - p) zuallererst unberücksichtigt bleiben. Dies gelingt mit der Variablen j, die zunächst den Wert 0 hat, dann aber nach der ersten Berechnung auf 1 gesetzt wird. In der Abb.3 ist eine Kreisbahn zu sehen, die mit dieser Korrektur gezogen wurde.

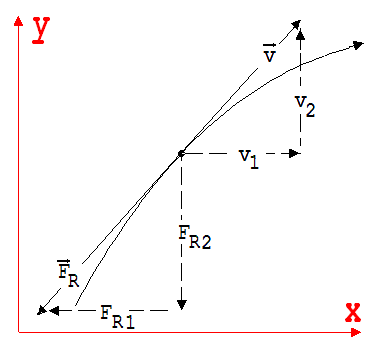
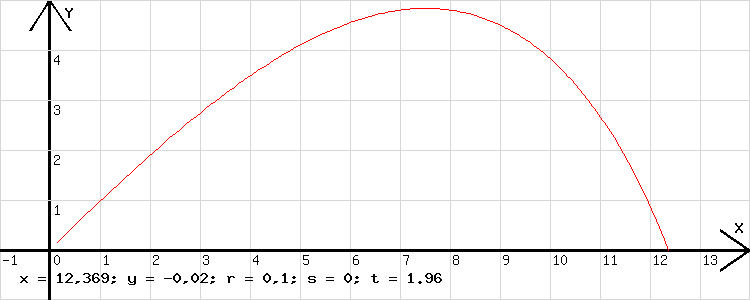
Schiefer Wurf unter Berücksichtigung der Luftreibung

Die Luftreibung muss berücksichtigt werden, wenn es darum geht, die Bahn einer Kanonenkugel zu bestimmen.

Welche Kraft wirkt auf die Kugel ?

|F_R| = k·v², v = |v| → F_R1 = - v₁ ·v · k ; F_R2 = - v₂ ·v · k

Neben der Reibungskraft wirkt noch die Gewichtskraft m·g. F₁ = - v₁· v · k und F₂ = - g· m - v₂ · v · k sind die x- und y-Koordinaten der auf die Kugel wirkenden Kraft. Zur Berechnung der Bahn mit dem hier vorliegenden Programm wird als Anfangswert für v₁ /(m/s) = c und v₂ /(m/s) = d der Wert 15, für den Reibungskoeffienten r / (kg/ m) der Wert 0,1 und für die Masse m/(kg) der Wert 1 eingetragen. Bei Bearbeitung der nachfolgenden Zeile liefert der Rechner die Wurfbahn in der Abb.5.

h=0,01; m=1; i=wrz(c^2+d^2); f=-c*i*r; g=-9,81*m-d*i*r; a=0,5*j*(f/m-o)+f/m; b=0,5*j*(g/m-p)+g/m; x=0,5*a*h^2+c*h+x; y=0,5*b*h^2+d*h+y; c=c+a*h; d=d+b*h; j=1; o=a; p=b; n=y;t=t+h

Mit n = y wird das Programm abgebrochen, sowie y < 0 ist, denn dann ist l = 0 größer als n.

Abb.5

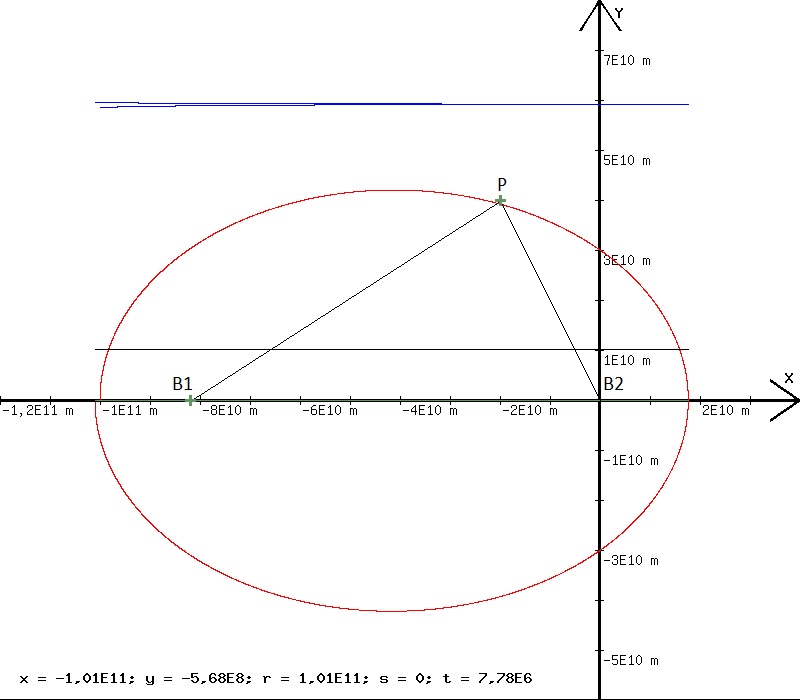
Zur Bewegung eines Planeten um die Sonne

Für die Beschleunigung eines Planeten unter der Anziehungskraft der Sonne gilt: a_x = - (G·M/r³)·x, a_y = - (G·M/r³)·y. G ist die Gravitationskonstante, M ist die Masse der Sonne und r ist der Abstand des Planeten von der Sonne. Die folgende Programmzeilen sind für eine Bewegung nach diesen Beschleunigungsgesetzen geschrieben.

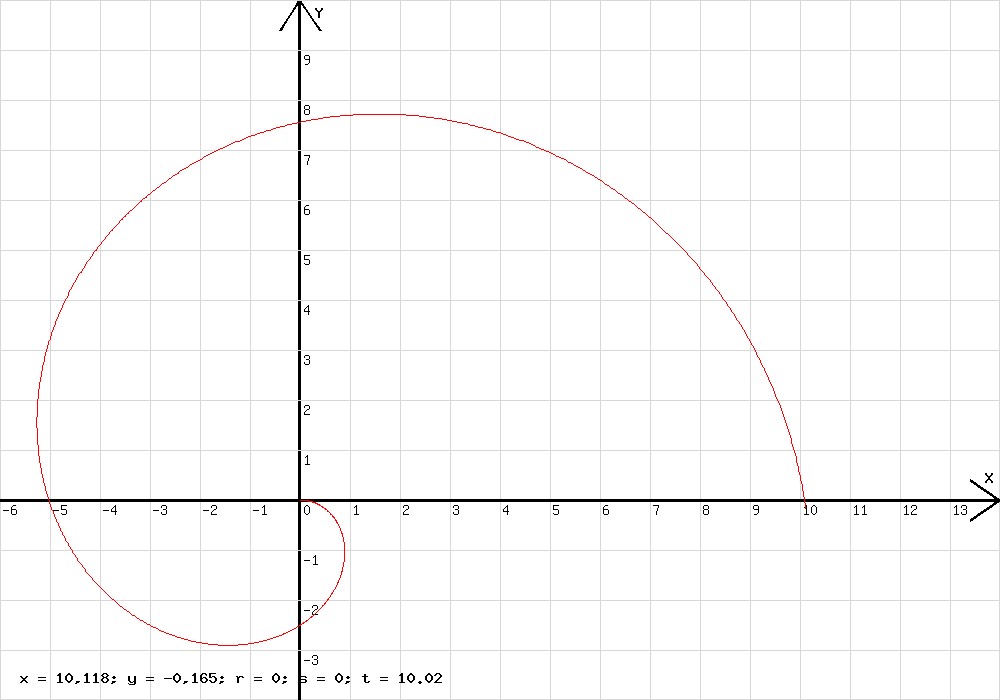
K=1,334E+20; h=778,35; r=wrz(x^2+y^2); a=-k/r^3*x; b=-k/r^3*y; a=0,5*j*(a-o)+a;b=0,5*j*(b-p)+b; x=0,5*a*h^2+c*h+x; y=0,5*b*h^2+d*h+y ; c=c+a*h; d=d+b*h; o=a;p=b; l=l+1; j=1; t=t+h; w=(r+wrz(y^2+(x+8,3E10)^2))/2; u=x; v =(y*c-x*d)*0,5*1E-5;

k Steht für G·M. Als Startpunkt wird der Punkt (-1E11m , 0) und als Startgeschwindigkeit v_y = d = 20000 m/s festgelegt.

w ist die halbe Summe aus den Abständen der Bahnpunkte von den beiden Brennpunkten B1 und B2. Sie wird von dem waagrechten blauen Diagramm angezeigt. Sie erweist sich als konstant. Die Bahn (siehe Abb. 6) ist somit eine Ellipse mit den Brennpunkten B1 und B2. Ebenfalls konstant ist die Flächengeschwindigkeit v =(y*c-x*d)*0,5. v/(1E5 m²/s) wird von dem schwarzen Diagramm angezeigt. Mit dieser Darstellung erfahren die beiden ersten Keplerschen Gesetze eine Bestätigung.

Abb.6

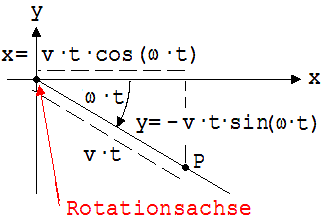
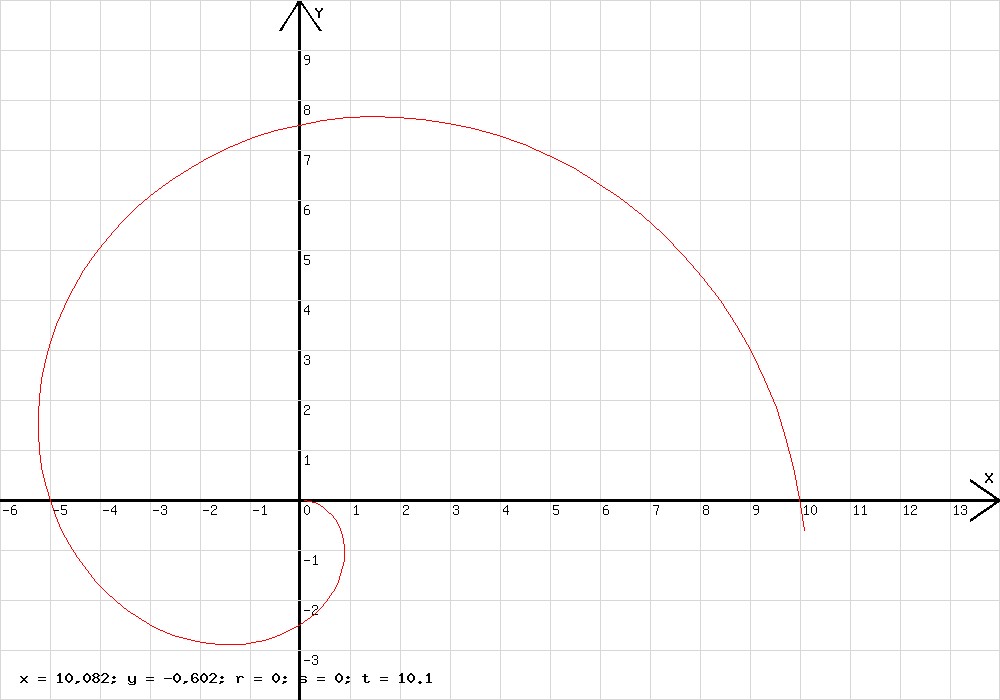
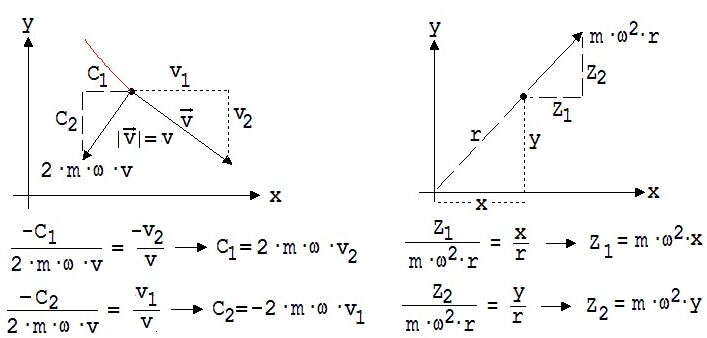
Berechnung einer Bewegung in einem rotierenden System unter Berücksichtigung der Zentrifugal- und Corioliskraft

Die Bewegung in einem rotierenden System wird nur dann richtig berechnet, wenn man neben den wirklichen Kräfte auch noch die Zentrifugal- und die Corioliskraft in die Rechnung eingehen lässt.

Beispiel: Wir stellen uns einen Massepunkt P vor, der sich auf einem ruhenden Strahl nach s = c·t (c = 1 m/s) von einem Punkt P entfernt. Wir denken uns dazu eine mit ω = 0,628 s ^-1 links herum rotierende, zum Strahl parallele Scheibe mit einer durch P gehenden Drehachse. Von der Scheibe aus gesehen wird dieser Strahl mit der Winkelgeschwindigkeit ω nach rechts gedreht und bildet zum Zeitpunkt t den Winkel ω·t mit der x-Achse des zum rotierenden System gehörenden x-y-Koordinatensystems (siehe Abb. 7). In der Abb. 8 ist die mit der Programmzeile „t=t+0,1; x=c*t*cos(0,628*t);y=-c*t*sin(0,628*t);l=t “ errechnete Bahn im rotierenden System dargestellt. Mit l=t zusammen mit dem Eintrag n= 10 im Variablenfeld wird t auf ungefähr 10 Sekunden begrenzt.

Für einen Beobachter im rotierenden System entsteht diese Bahn unter der Wirkung der Zentrifugalkraft Z = {Z₁; Z₂}= und der Corioliskraft C = {C₁; C₂} , deren Koordinaten wie folgt bestimmt werden.

Mit den folgenden Programmzeilen wurde die Bahn (siehe Abb. 10) berechnet, die im rotierenden System unter Einwirkung der Corioliskraft und der Zentrifugalkraft zu erwarten ist.

h=0,01; a=2*0,628*d+0,628^2*x; b=-2*0,628*c+0,628^2*y; a=0,5*j*(a-o)+a;b=0,5*j*(b-p)+b; x=0,5*a*h^2+c*h+x; y=0,5*b*h^2+d*h+y ; c=c+a*h; d=d+b*h; o=a;p=b; l=t; j=1; t=t+h .

c und d stehen für v₁ und v₂ , a und b für die Beschleunigungen a₁ und a₂. Als Anfangswert von c wurde in dem hier vorliegenden Beispiel der Wert 1/(m/s) gewählt. Die Bahn in der Abb. 8 stimmt mit der in der Abb.10 überein.

Über das Auslaufen einer Badewanne

Eine quaderförmige Badewanne mit dem Querschnitt A = 0,8 m² läuft durch eine Öffnung am Boden mit dem Querschnitt B aus.

B = 10 cm² = 0,001 m², anfängliches Wasservolumen = 0,15 m³.

Abb.11

1. Mit welcher Geschwindigkeit tritt das Wasser aus dieser Öffnung ?

2. In welcher Zeit wird die Badewanne geleert ?

Diese beiden Fragen können mit Hilfe des Energiesatzes beantwortet werden. Auf die Frage 1 ist schnell eine Antwort gefunden. Wenn eine kleine Wassermenge der Masse m’ ausläuft, dann fehlt sie an der Oberfläche des Wassers. Die potentielle Energie des Wassers nimmt um m’·g · x ab (x = Höhe des Wasserspiegels). Das unten austretende Wasser hat die kinetische Energie m’ ·v² /2 . Nach dem Energieerhaltungssatz gilt:

m’ ·v² /2 = m’ · g · x → v = √( 2 · g · x )

x ·A = V  → x = V/A, v = √( 2 · g · x)  → v = √( 2 · g · V/A )

Die kinetische Energie des Wassers infolge der Sinkgeschwindigkeit ist vernachlässigbar klein. Aus dem Wasservolumen V und dem Querschnitt A der Badewanne kann x errechnet werden. Nach einem kleinen Zeitabschnitt Δt = h hat das Volumen der Wassers um v · Δt ·B abgenommen (siehe Abb. 12).

Für das Volumen V' nach Δt gilt: V' = V - √( 2 · g · V/A ) · Δt ·B.

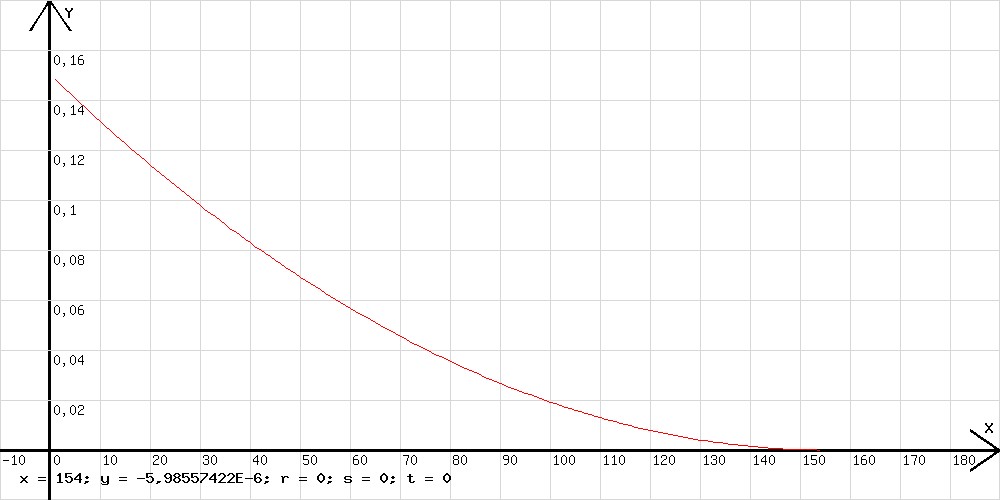
Abb.12

Mit y = y - wrz( 2 * 9,81 * y/0,8 ) * h*0,001 ; x=x+h;l=x; wird das Volumen in Abhängigkeit von der Zeit angezeigt (siehe Abb. 13).

Als Anfangswert von y muss 0,15 eingetragen werden.

Mit y = y - wrz( 2 * 9,81 * y/0,8 ) * h*0,001 ; x=x+h;l=x; w=6,25E-6*(x-155)^2 wird außerdem noch eine Parabel dem Auslaufdiagramm angepasst (siehe Abb. 14).

In Abb. 13 ist zu sehen, dass eine Wanne mit einem Querschnitt A =0,8 m² , welche anfangs 0,15 m³  Wasser enthält, in ca. T =155 s durch ein Loch mit dem Querschnitt B = 10 cm² leer läuft.

Abb.13

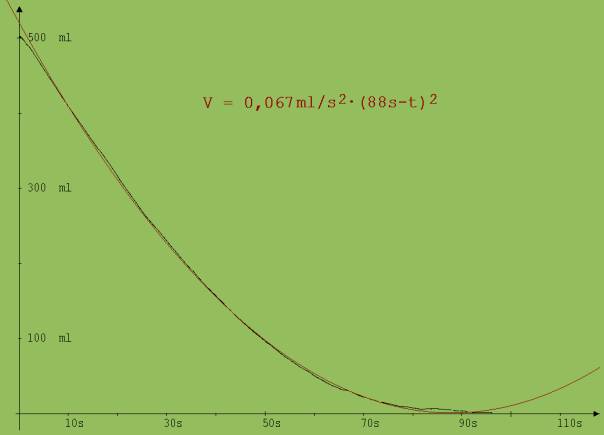
Abb. 14

In der Abb. 15 ist ein Messdiagramm  zu sehen, welches von einem Schüler (Adalbert-Stifter-Gymnasium in Passau)  im Rahmen einer Facharbeit mit Hilfe der Experimentierwippe aufgenommen wurde. Der Schüler ließ ein an der Schmalseite der Experimentierwippe hängendes,  mit  Wasser gefülltes zylindrisches Gefäß ( Durchmesser = 8 cm) mit einem Loch im Gefäßbodenboden (Durchmesser 3,2 mm) leer laufen. Die Wippe diente in diesem Fall als elektrische Waage. Dem Diagramm ist eine Parabel nach V = f(t) = 0,067 ml/s² ·(88 s – t)² angepasst.

Abb.15

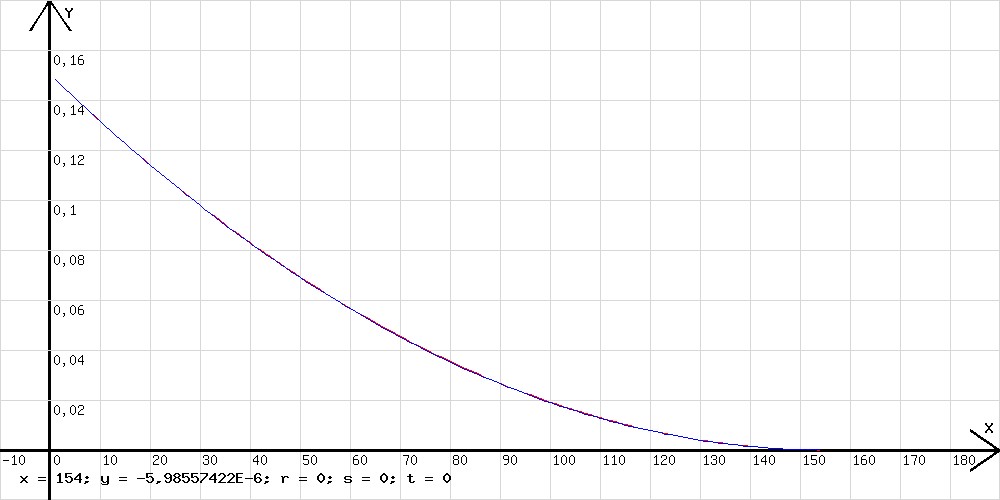
Über das Auslaufen eines Gefäßes mit textilem Boden

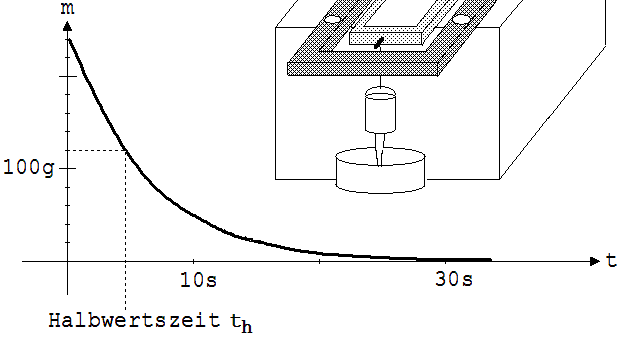
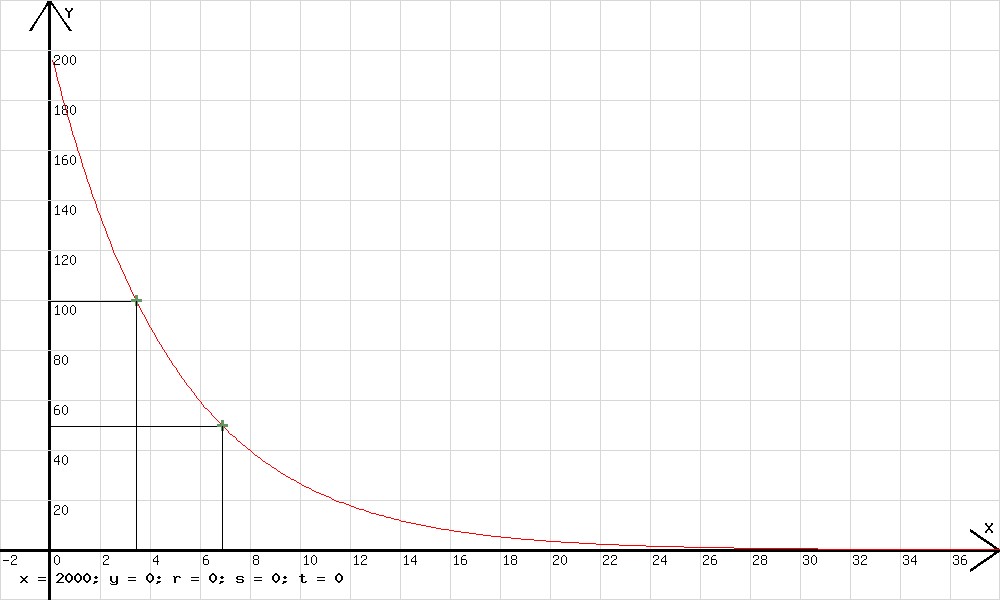
Abb.16

An der freien Schmalseite der Experimentierwippe (siehe Abb. 16) hängt ein Gefäß mit textilem Boden. Aus diesem Gefäß läuft Wasser aus, wobei der Rechner das Diagramm in der Abb. 16 aufzeichnet. Wie an dem Diagramm erkennbar, läuft in einer Zeit t_h, der sogenannten Halbwertszeit, unabhängig vom anfänglichen Wasserstand die Hälfte der Wassermenge aus.

Im ersten Zeitabschnitt der Dauer t_h nimmt die Wassermasse m₀ auf m₀/2 ab. Am Ende des darauf folgenden Zeitabschnitts der gleicher Dauer hat der Gefäßinhalt die Masse m = m₀·(1/2)·(1/2) und nach der Zeit t = n·t_h ( n = t/t_h ) gilt :

m = m₀ · (1/2)ⁿ = m₀ · (1/2)^(t/th) = m₀ · 2 ^{- (t/th)}

Eine Exponentialfunktion beschreibt das Ausfließen des Wassers .

Mit Hilfe des vorliegenden Grafikprogramm kann man dieses Auslaufverhalten erklären, wenn man davon ausgeht, dass der textile Boden das Auslaufen mit einer der Auslaufgeschwindigkeit v proportionalen Kraft F_R bremst.

v ~ Δm/Δt , Δm ist die Masse der in dem kleinen Zeitabschnitt Δt austretenden Flüssigkeit.

v ~ F_R , Δm/Δt ~ v → Δm/Δt ~ F_R → (Δm/Δt) / F_R = Konstante = k → Δm/Δt = k · F_R , Δm = k · F_R  · Δt

Die auf das Wasser insgesamt wirkende Kraft ist m·g - F_R . → m·g - F_R = m·a (m·g : Gewichtskraft, a: Beschleunigung des Wassers). Da die Beschleunigung des absinkenden Wassers vernachlässigbar klein ist, kann geschrieben werden: m·g = F_R. _.

Wenn das Wasser vor Δt die Masse m hatte, dann ist m' = m – Δm = m - k · m ·g · Δt = m ·( 1- k · g · Δt ) die Masse m' nach Δt.

Zur Simulation dieses Vorgangs wird in das Rechenfenster des genannten Programms folgende Zeile eingetragen: y=y*(1-k*g*h); x=x+h;. g steht für 9,81 m/s², y für die Masse, x für die Zeit t und h für Δt. Für h wird 0,01 (0,01 s), für k der Wert 0,02 (0,02 s/m) und für den Anfangswert von y der Wert 200 (200g) eingetragen. Danach entsteht ein Diagramm, wie es in der Abb. 17 zu sehen ist. Es ist erkennbar, dass auch in diesem simulierten Fall die Halbwertszeit unabhängig von der anfangs vorhandenen Wassermenge ist.

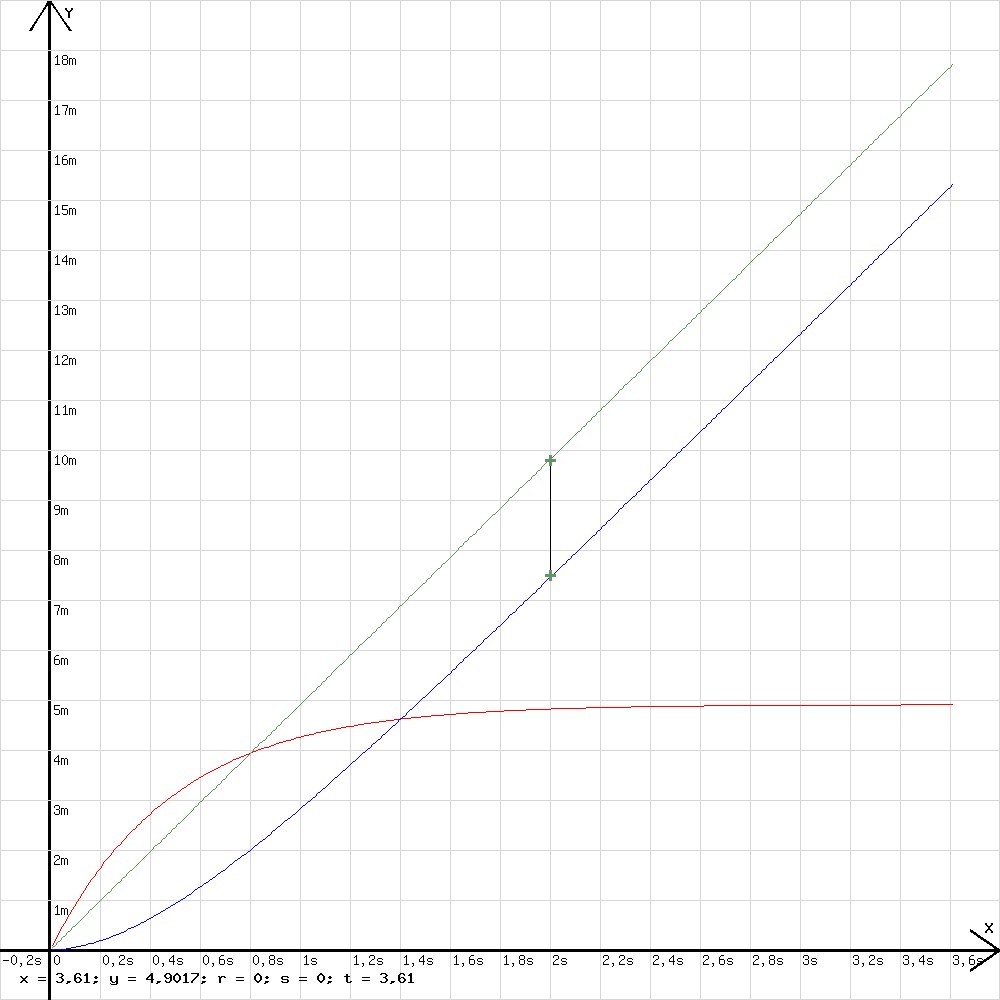
Abb. 17

Fallbewegung in einer Flüssigkeit

Wir stellen uns eine in Öl fallende Eisenkugel vor (Fallbeginn zum Zeitpunkt t = 0). Der Gewichtskraft m · g wirkt eine der Geschwindigkeit proportionale Reibungskraft F_R = k ·v entgegen.. Die Geschwindigkeit wächst solange bis die Gewichtskraft gleich der Reibungskraft ist.

Wie ändert sich die Geschwindigkeit v mit der Zeit ?

F_R /v = k (Konstante)   →   F_R = k·v 

Für die Beschleunigung a gilt demnach:   m· a = m· g – k · v    →    a = g – k· v/m

Die Diagramme in der Abb. 18 zur zeitliche Entwicklung der Geschwindigkeit und des zurückgelegten Weges der Kugel ­ wurden mit der folgenden Zeile im Rechenfenster des hier vorhandenen erhalten:

k=2; m=1; h=0,01; a=9,81-k/m*c; c=c+a*h; x=x+h; l=x; y=c; w=c*h+w; z= m*9,81/k*x;

c= v , x=t !

Abb.18

Das rote Diagramm ist das v-t-Diagramm (y-t-Diagramm), das weiße das zugehörende s-t-Diagramm (w-t-Diagramm).

Die Endgeschwindigkeit v_Ende ist dann erreicht, wenn die Reibungskraft gleich der Gewichtskraft ist.

↓

  m ·g = k · v_Ende     →     v_Ende = m ·g / k

Hätte die Bewegung mit der Endgeschwindigkeit begonnen, dann wäre sie gleichförmig nach dem grünen Diagramm (z-t-Diagramm) verlaufen.

Das Verhältnis v/ v_Ende = v·k /(m· g) ist ein Wert f der nach dem Beginn der Bewegung von 0 auf 1 ansteigt. Für die Geschwindigkeit v kann  v = m·g/k ·f  geschrieben werden.  Der Term (1 - e ^{– j ·t} ) mit einer noch unbekannten Konstanten j  kommt als Faktor f in Frage. Je größer j ist, desto schneller wird die Endgeschwindigkeit erreicht. Es ist davon auszugehen, dass eine große Reibungskraft und eine geringe Gewichtskraft in kurzer Zeit zur Endgeschwindigkeit führen.

Vermutung: j = k/m    →  v = m · g/k · (1- e^{- (k/m) · t})

Mit der folgenden Zeile wird diese Vermutung bestätigt. Die Diagramme zu y und v stimmen überein.

k=2; m=1; h=0,01; a=9,81-k/m*c; c=c+a*h; x=x+h; l=x; y=c; w=c*h+w; z= m*9,81/k*x; v=m*9,81/k*(1-exp(-k/m*x)); u=x 

Hätte der Körper schon zu Anfang  die Höchstgeschwindigkeit m ·g/k,  dann wäre  s = m · (g/k) ·t . Für s gilt jedoch  s < m·(g/k)·t. Die mit der senkrechten Strecke in der bei 2 Sekunden in der Abb. 18 angedeutete Differenz d zwischen m·(g/k)·t und dem wahren Weg s wird sich vermutlich nach dem Bewegungsbeginn ähnlich wie die Geschwindigkeit zu einem Maximalwert entwickeln .

Vermutung : m · (g/ k) · t – s = r · (1 - e ^{– k · t/m} )

Der unbekannte Faktor r  muss  von m, g und k abhängen und die Einheit eines Weges haben. Vermutlich ist  r = m² / k² · g , denn m²/k² · g  hat die Einheit eines Weges.

→  s = m · g/ k · t -  m² / k² · g ·  (1 - e ^{– k · t/m} )

Zur Prüfung dieser Annahme wird das Grafikprogramm mit „k=2; m=1; h=0,01; a=9,81-k/m*c; c=c+a*h; x=x+h; l=x; y=c; w=c*h+w; z=m*9,81/k*x; v=m*9,81/k*x-m^2/k^2*9,81*(1-exp(-k*x/m)); u=x“  gestartet. Dabei wird das ursprüngliche, blaue Weg-Zeit-Diagramm überzeichnet.